Sort-merge join
The Sort-Merge Join (also known as Merge-Join) is an example of a join algorithm and is used in the implementation of a relational database management system.
The basic problem of a join algorithm is to find, for each distinct value of the join attribute, the set of tuples in each relation which display that value. The key idea of the Sort-merge algorithm is to first sort the relations by the join attribute, so that interleaved linear scans will encounter these sets at the same time.
In practice, the most expensive part of performing a sort-merge join is arranging for both inputs to the algorithm to be presented in sorted order. This can be achieved via an explicit sort operation (often an external sort), or by taking advantage of a pre-existing ordering in one or both of the join relations. The latter condition can occur because an input to the join might be produced by an index scan of a tree-based index, another merge join, or some other plan operator that happens to produce output sorted on an appropriate key.
Let's say that we have two relations  and
and  and
and  .
.  fits in
fits in 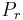 pages memory and
pages memory and  fits in
fits in 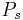 pages memory. So, in the worst case Sort-Merge Join will run in
pages memory. So, in the worst case Sort-Merge Join will run in  I/Os. In the case that
I/Os. In the case that  and
and  are not ordered the worst case will be
are not ordered the worst case will be  (where the last two terms are the cost of ordering both of them first).
(where the last two terms are the cost of ordering both of them first).
Pseudocode
For simplicity, the algorithm is described in the case of an inner join of two relations on a single attribute. Generalization to other join types, more relations and more keys is straightforward.
function sortMerge(relation left, relation right, attribute a)
var relation output
var list left_sorted := sort(left, a) // Relation left sorted on attribute a
var list right_sorted := sort(right, a)
var attribute left_key, right_key
var set left_subset, right_subset // These sets discarded except where join predicate is satisfied
advance(left_subset, left_sorted, left_key, a)
advance(right_subset, right_sorted, right_key, a)
while not empty(left_subset) and not empty(right_subset)
if left_key = right_key // Join predicate satisfied
add cross product of left_subset and right_subset to output
advance(left_subset, left_sorted, left_key, a)
advance(right_subset, right_sorted, right_key, a)
else if left_key < right_key
advance(left_subset, left_sorted, left_key, a)
else // left_key > right_key
advance(right_subset, right_sorted, right_key, a)
return output
// Remove tuples from sorted to subset until the sorted[1].a value changes
function advance(subset out, sorted inout, key out, a in)
key := sorted[1].a
subset := emptySet
while not empty(sorted) and sorted[1].a = key
insert sorted[1] into subset
remove sorted[1]
Simple C# Implementation
Note that this implementation assumes the join attributes are unique, i.e., there is no need to output multiple tuples for a given value of the key.
public class MergeJoin { // Assume that left and right are already sorted public static Relation Sort(Relation left, Relation right) { Relation output = new Relation(); while (!left.IsPastEnd() && !right.IsPastEnd()) { if (left.Key == right.Key) { output.Add(left.Key); left.Advance(); right.Advance(); } else if (left.Key < right.Key) left.Advance(); else //(left.Key > right.Key) right.Advance(); } return output; } } public class Relation { private List<int> list; public const int ENDPOS = -1; public int position = 0; public int Position { get { return position; } } public int Key { get { return list[position]; } } public bool Advance() { if (position ==list.Count - 1 || position== ENDPOS) { position = ENDPOS; return false; } position++; return true; } public void Add(int key) { list.Add(key); } public bool IsPastEnd() { return position == ENDPOS; } public void Print() { foreach (int key in list) Console.WriteLine(key); } public Relation(List<int> list) { this.list = list; } public Relation() { this.list = new List<int>(); } }
External links
C# Implementations of Various Join Algorithms [1]